Théorème de Pythagore

Nous expliquons ce qu’est le théorème de Pythagore, comment est sa formule et son explication. Aussi, quelles sont ses caractéristiques, ses utilisations et ses exemples.

Qu’est-ce que le théorème de Pythagore ?

Le théorème de Pythagore est un postulat mathématique formulé par le philosophe et mathématicien grec Pythagore de Salmos (c. 569 – c. 475 av. J.-C.), un étudiant des lois des mathématiques dont les contributions à l’arithmétique et à la géométrie persistent à ce jour. Ce postulat dit que la somme du carré des côtés d’un triangle rectangle est toujours égale au carré de son hypoténuse.

Cette proposition est, sans aucun doute, l’une des plus connues de l’histoire des mathématiques , et celle qui a le plus grand nombre de démonstrations à travers le temps, à travers différentes méthodes et élaborées par divers philosophes et mathématiciens.

Selon certains auteurs , jusqu’à un millier de preuves différentes peuvent être trouvées , bien que 367 aient été officiellement cataloguées, car la preuve du théorème était une exigence au Moyen Âge pour obtenir le titre de Magister matheseos (« Maître en Mathématiques »). ) à l’académie. .

Voir aussi : Vecteurs

Histoire du théorème de Pythagore

Bien que la paternité du théorème soit attribuée au grec Pythagore , puisque sa démonstration était d’une importance capitale pour les philosophes pythagoriciens (disciples formés dans un culte quasi religieux des mathématiques), la vérité est que l’origine de ce théorème est bien antérieure.

Des preuves de son utilisation existent dans les tablettes babyloniennes et les papyrus de l’Égypte ancienne , mais aucun document exposant leur relation n’a survécu à ce jour. On sait que l’étude des triangles était au cœur de nombreuses cultures anciennes .

Préceptes de base du théorème de Pythagore

Pour commencer avec le théorème de Pythagore, il faut comprendre que les jambes d’un triangle rectangle qui forment l’angle droit (90°) sont appelées jambes et le côté restant et le plus long s’appelle l’ hypoténuse .

Formule du théorème de Pythagore

Le théorème de Pythagore est formulé comme suit : a ² + b ² = c ²  où a et b sont les branches d’un triangle rectangle et où c est son hypoténuse. Trois corollaires ou formulations ultérieures découlent de cette formulation, d’application pratique et de vérification algébrique :

• a = √ c ² – b ² ( a est égal à la racine carrée de c au carré moins b au carré)
• b = √b ² – a ² ( b est égal à la racine carrée de c au carré moins a au carré)
• c = √a ² + b ² ( c est égal à la racine carrée de a au carré plus b au carré)

Explication du théorème de Pythagore

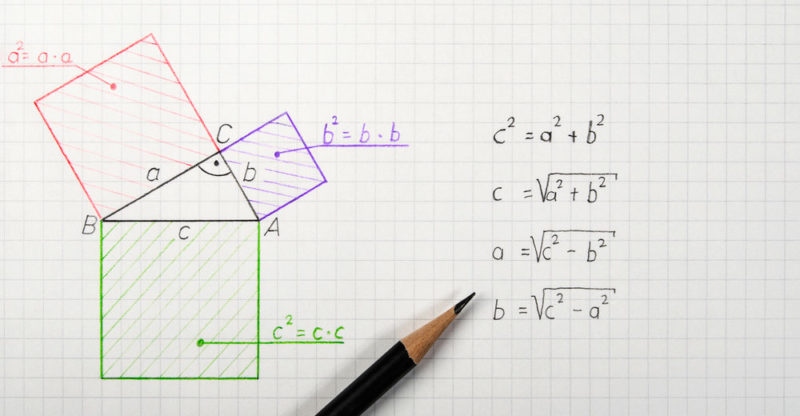
La logique du théorème de Pythagore est assez simple et évidente. Étant donné un triangle de côtés a, b et c, dans lequel a et b forment un angle droit (c’est-à-dire 90°), il est possible de calculer la longueur de l’hypoténuse en additionnant les carrés des jambes o, n’importe lequel des côtés du triangle.

Exemple du théorème de Pythagore

Un exemple simple d’application du théorème est le suivant :

• Étant donné un triangle rectangle dont les jambes a et b mesurent respectivement 3 et 4 cm, on peut calculer son hypoténuse c en substituant les valeurs dans la formule, comme suit :

c2 = ^a2 + ^{b2 _}

alors c ² = 3 ² + 4 ²

et donc c2 = 9 + 16 = 25

et enfin c = √25 = 5

L’hypoténuse c mesure 5 cm

Preuves du théorème de Pythagore

Les preuves du théorème de Pythagore sont aussi variées que nombreuses, mais celles proposées par Euclide (325-265 avant JC), Pappus d’Alexandrie (290-350 avant JC), Bhaskara II de l’Inde (114-1185 après JC), Léonard de Vinci (1452-1519 après JC) et James Garfield (1831-1881).

Chacun utilisait des méthodes géométriques et arithmétiques différentes qui, cependant, conduisaient toujours à la même confirmation du théorème.

Preuve réciproque du théorème de Pythagore

Il est possible d’utiliser ce théorème dans son sens inverse, pour vérifier si un triangle donné est un triangle rectangle (dans les cas, par exemple, où il ne peut pas être représenté graphiquement).

C’est extrêmement simple : si dans un triangle quelconque il s’avère vrai que la somme du carré de ses jambes est égale au carré de l’hypoténuse , alors les deux premiers formeront nécessairement un angle droit et nous serons en présence d’un triangle rectangle.

Applications du théorème de Pythagore

Les applications de ce théorème sont nombreuses dans le domaine de l’ingénierie, de l’architecture et de la géométrie en général . Depuis l’Antiquité, l’étude du triangle à des fins pratiques a donné des résultats tangibles, comme les fameuses pyramides égyptiennes.

Toute situation de calcul dans laquelle nous sommes en présence d’un triangle rectangle permettra l’application de ce théorème pour calculer l’un de ses côtés.

Importance pour les autres domaines

D’autres domaines des mathématiques peuvent utiliser ce théorème pour leurs calculs. Par exemple:

• Géométrie analytique plane. Ce théorème est utilisé pour trouver la distance entre des points sur un plan cartésien.
• Trigonométrie. Nous utilisons ce théorème pour prouver l’identité fondamentale  sin2 ^a + cos2 ^a = 1.

Exercices sur le théorème de Pythagore

Voici deux exercices à ce sujet :

• Etant donné l’hypoténuse de 20 cm dans un triangle rectangle dont on sait aussi qu’une de ses jambes mesure 5 cm, que mesurera la jambe restante ?
• Si vous avez besoin de faire une rampe sur une marche d’escalier et que l’on sait que la hauteur de la marche est de 30 cm et la longueur de la marche est de 1 m, quelle doit être la longueur du plan incliné de la rampe ?

Continuer avec : Polygones