Nous expliquons ce qu’est un quadrilatère et comment ce polygone est classé. Aussi, quelles sont ses principales caractéristiques et quelques exemples.
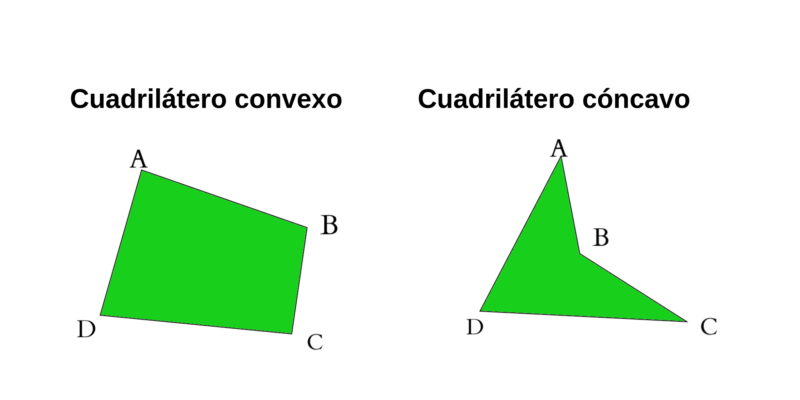
Que sont les quadrilatères ?
Les quadrilatères sont des polygones (figures géométriques planes) à quatre côtés et deux diagonales . Ils sont caractérisés par quatre sommets et quatre angles, et la somme de leurs angles internes est toujours de 360°. Par exemple : un carré, un trapèze ou un losange.
Ces figures sont également connues sous le nom de quadrangles et sont utilisées dans des disciplines telles que la géométrie. Le mot quadrilatère dérive des termes latins quadri (quatre) et latus (côtés).
Voir aussi: théorème de Pythagore
Caractéristiques des quadrilatères
Certaines des principales caractéristiques des quadrilatères sont :
- Ce sont des polygones, c’est-à-dire des figures géométriques fermées et plates formées de côtés et de sommets.
- Ils peuvent être simples ou complexes et dans tous les cas ils ont quatre côtés et quatre sommets.
- Ils peuvent avoir des formes différentes et avoir toujours deux diagonales.
- Ils ont quatre angles extérieurs et quatre angles intérieurs (qui totalisent 360°).
- Ils sont classés selon la somme de leurs angles intérieurs comme concaves et convexes.
- Selon le parallélisme de leurs côtés ils peuvent être : des parallélogrammes, des trapèzes ou des trapèzes.
éléments de quadrilatères
Les quadrilatères sont caractérisés par les éléments suivants :
- côtés . Ce sont des lignes ou des segments qui joignent les sommets et qui peuvent ou non être égaux les uns aux autres.
- sommets . Ce sont les points d’intersection des côtés. Chaque quadrilatère a quatre sommets.
- Diagonales . Ce sont des segments qui relient des sommets opposés.
- angles intérieurs . Ce sont les angles visibles qui sont déterminés par les côtés qui les composent. Les angles intérieurs d’un quadrilatère totalisent 360°.
- Angles extérieurs . Ce sont les angles formés avec des lignes imaginaires (côtés) qui continuent les lignes du quadrilatère.
types de quadrilatère
Les quadrilatères peuvent être classés en fonction de leur forme en quadrilatères complexes et en quadrilatères simples.
- Quadrilatères complexes . Ce sont ceux dont deux de leurs côtés se coupent.
- Quadrilatères simples . Ce sont ceux dont les côtés ne se coupent pas et peuvent être :
- Quadrilatères concaves . Ce sont des quadrilatères qui ont un angle supérieur à 180°.
- Quadrilatères convexes . Ce sont des quadrilatères qui n’ont pas d’angles intérieurs de 180° ou plus.
- Quadrilatères croisés . Ce sont des quadrilatères qui ont des côtés qui se coupent ou se coupent.
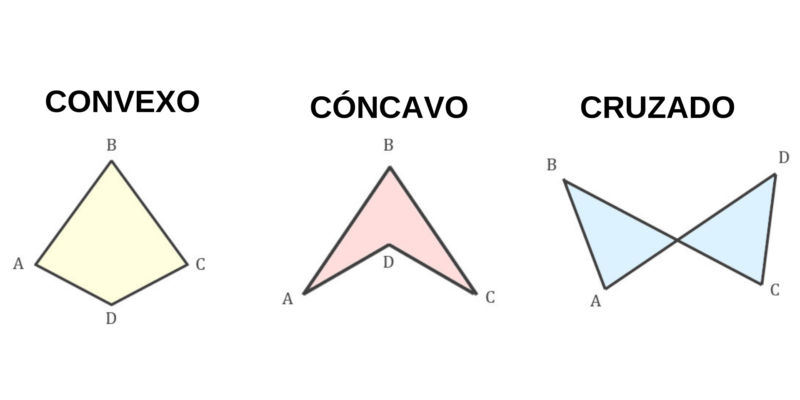
Les quadrilatères convexes peuvent être :
- parallélogrammes
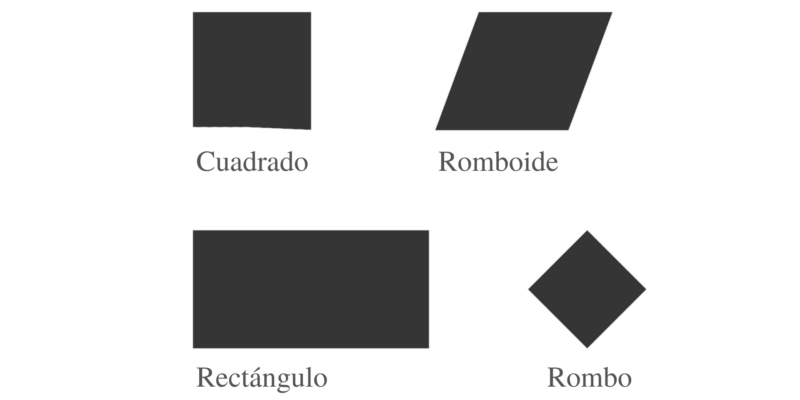
Ce sont des quadrilatères qui ont deux paires de côtés parallèles et dont les côtés opposés sont identiques. De plus, les angles internes opposés sont égaux entre eux et les diagonales se coupent en leur point médian. Quelques exemples sont:
- rhomboïde . Quadrilatère dont les quatre côtés ne forment pas des angles droits et dont les côtés opposés sont égaux.
- losange . Quadrilatère dont les quatre côtés sont égaux mais ne forment pas d’angles droits.
- rectangle . Quadrilatère qui a quatre côtés et dont chaque paire de côtés parallèles a la même mesure. Comme les carrés, ils ont quatre angles droits.
- carré . Quadrilatère ayant quatre côtés égaux et quatre angles droits.
- trapèzes
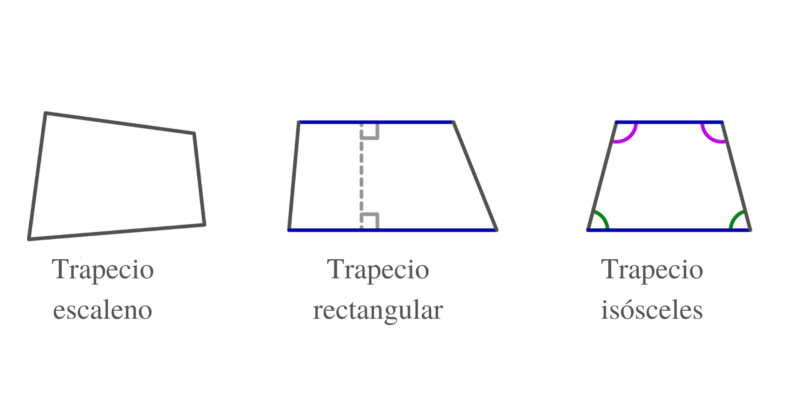
Ce sont des quadrilatères qui ont deux côtés parallèles , qu’on appelle la grande base et la petite base. Les trapèzes peuvent être :
- Trapèze scalène . Il a ses quatre angles internes inégaux.
- Trapèze isocèle . Il a des côtés égaux non parallèles.
- Trapèze rectangulaire . Il a deux angles internes droits et deux qui ne sont pas droits.
Plus dans: Trapèze
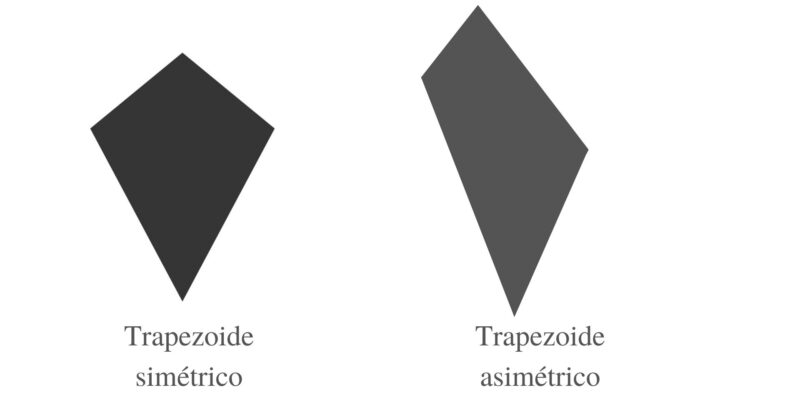
- trapèzes
Ce sont des quadrilatères qui n’ont aucun de leurs côtés parallèles entre eux. Ils sont divisés en :
- Trapèzes symétriques . Ils ont un axe de symétrie interne
- Trapèzes asymétriques ou amorphes . Ils n’ont pas d’axe de symétrie interne.
Cela peut vous aider : Vecteurs